Doplněk Řešitel aplikace Excel provádí matematickou optimalizaci. To se obvykle používá k přizpůsobení složitých modelů datům nebo k nalezení iterativních řešení problémů. Můžete například chtít přizpůsobit křivku některými datovými body pomocí rovnice. Řešitel může najít v rovnici konstanty, které nejlépe odpovídají datům. Jinou aplikací je situace, kdy je obtížné změnit uspořádání modelu tak, aby se požadovaný výstup stal předmětem rovnice.
Kde je řešitel v aplikaci Excel?
Doplněk Řešitel je součástí aplikace Excel, ale ne vždy se načte jako součást výchozí instalace. Chcete-li zkontrolovat, zda je načteno, vyberte ikonu DATA kartu a vyhledejte Řešitel ikona v Analýza sekce.
Pokud na kartě DATA nemůžete najít Řešitele, budete muset načíst doplněk:
-
Vybrat SOUBOR kartu a poté vyberte Možnosti.
-
V Možnosti vyberte dialogové okno Doplňky ze záložek na levé straně.
-
V dolní části okna vyberte Doplňky aplikace Excel z Spravovat rozevírací seznam a vyberte Jít…
-
Zaškrtněte políčko vedle Doplněk Řešitele a vyberte OK.
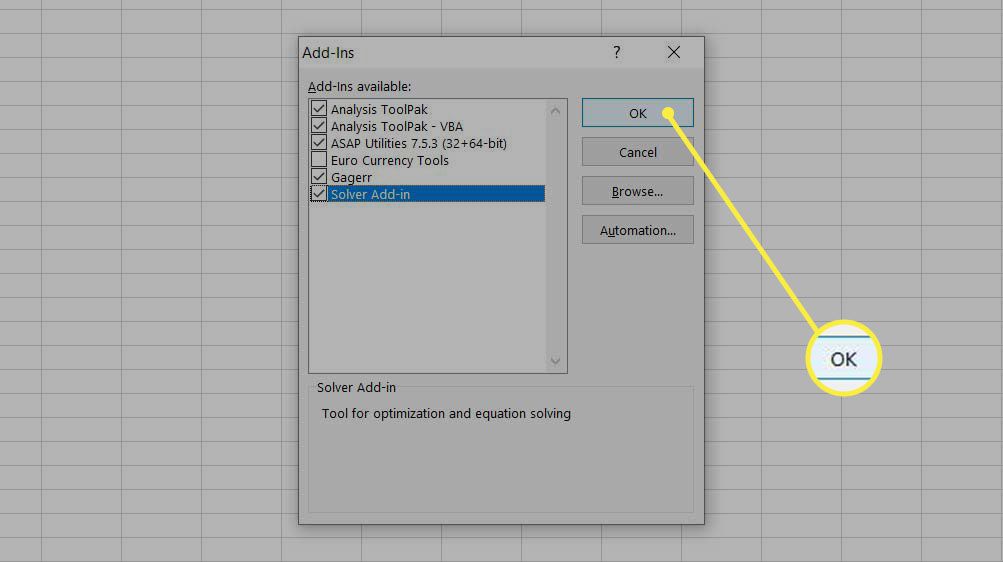
-
The Řešitel příkaz by se nyní měl objevit na DATA záložka. Jste připraveni použít Řešitel.
Používání Řešitele v aplikaci Excel
Začněme jednoduchým příkladem, abychom pochopili, co Řešitel dělá. Představte si, že chceme vědět, jaký poloměr dá kružnici o ploše 50 čtverečních jednotek. Známe rovnici pro plochu kruhu (A = pi r2). Tuto rovnici bychom samozřejmě mohli přeskupit, abychom dostali poloměr požadovaný pro danou oblast, ale pro příklad si předstírejme, že nevíme, jak to udělat. Vytvořte tabulku s poloměrem dovnitř B1 a vypočítat plochu v B2 pomocí rovnice = pi () * B1 ^ 2.
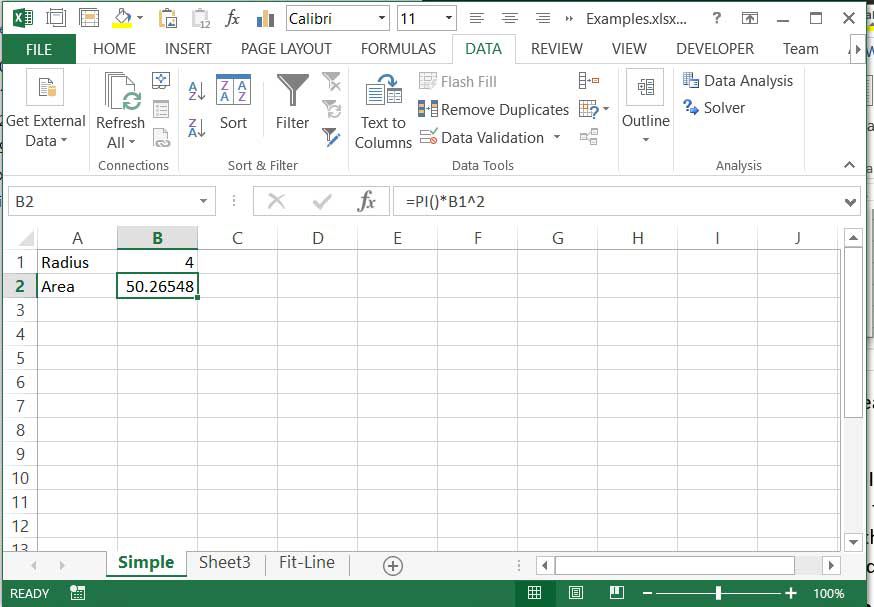
Hodnotu jsme mohli upravit ručně B1 dokud B2 ukazuje hodnotu, která je dostatečně blízká 50. V závislosti na tom, jak přesné musíme být, může jít o praktický přístup. Pokud však potřebujeme být velmi přesní, provedení požadovaných úprav bude trvat dlouho. Ve skutečnosti je to v podstatě to, co Řešitel dělá. Provádí úpravy hodnot v určitých buňkách a kontroluje hodnotu v cílové buňce:
-
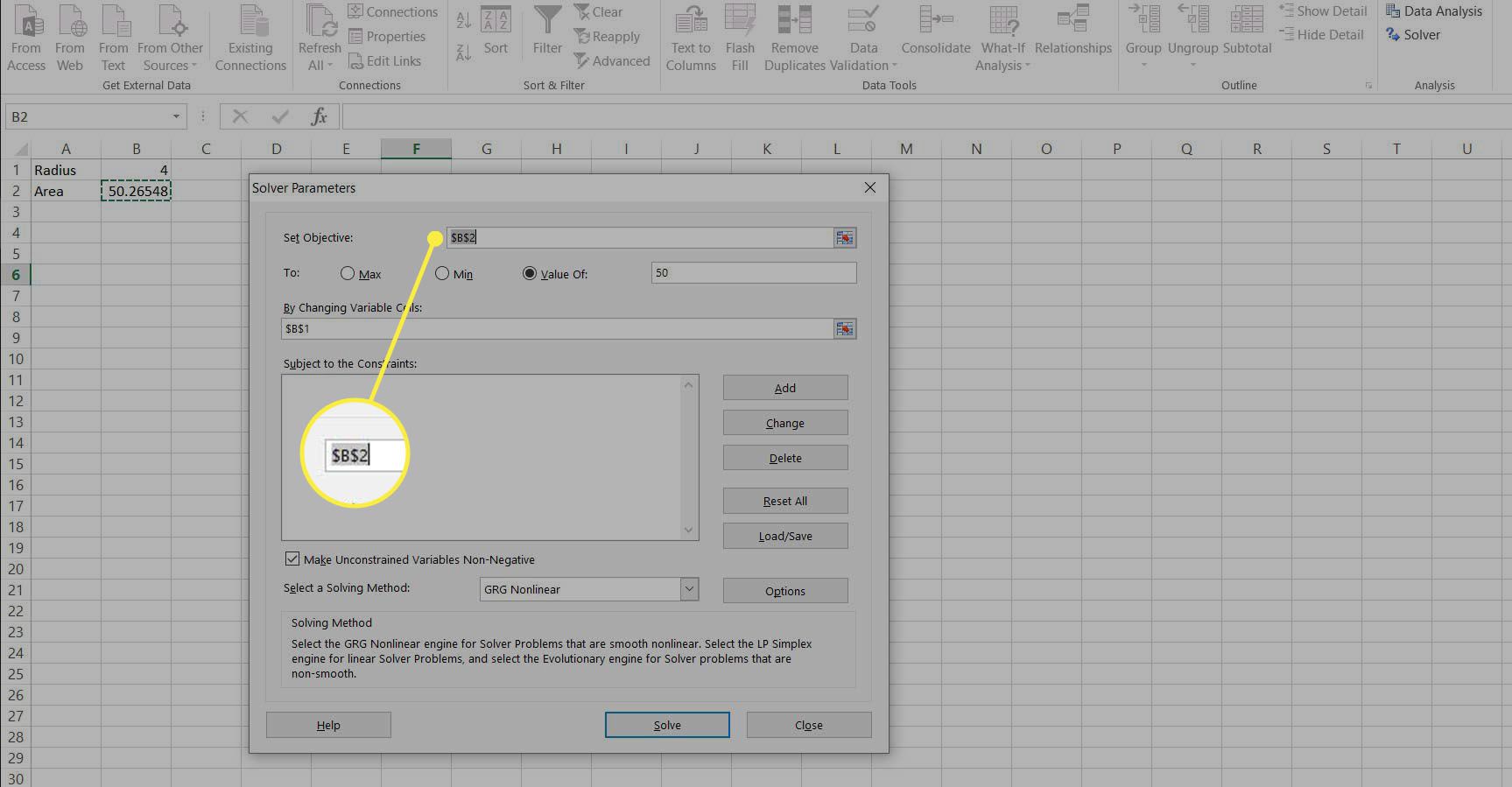
Vybrat DATA karta a Řešitel, načíst Parametry řešiče dialogové okno
-
Stanovit cíl buňka být Oblast, B2. Toto je hodnota, která bude zkontrolována a upraví další buňky, dokud tato nedosáhne správné hodnoty.
-
Vyberte tlačítko pro Hodnota: a nastavte hodnotu 50. To je hodnota, které by měl B2 dosáhnout.
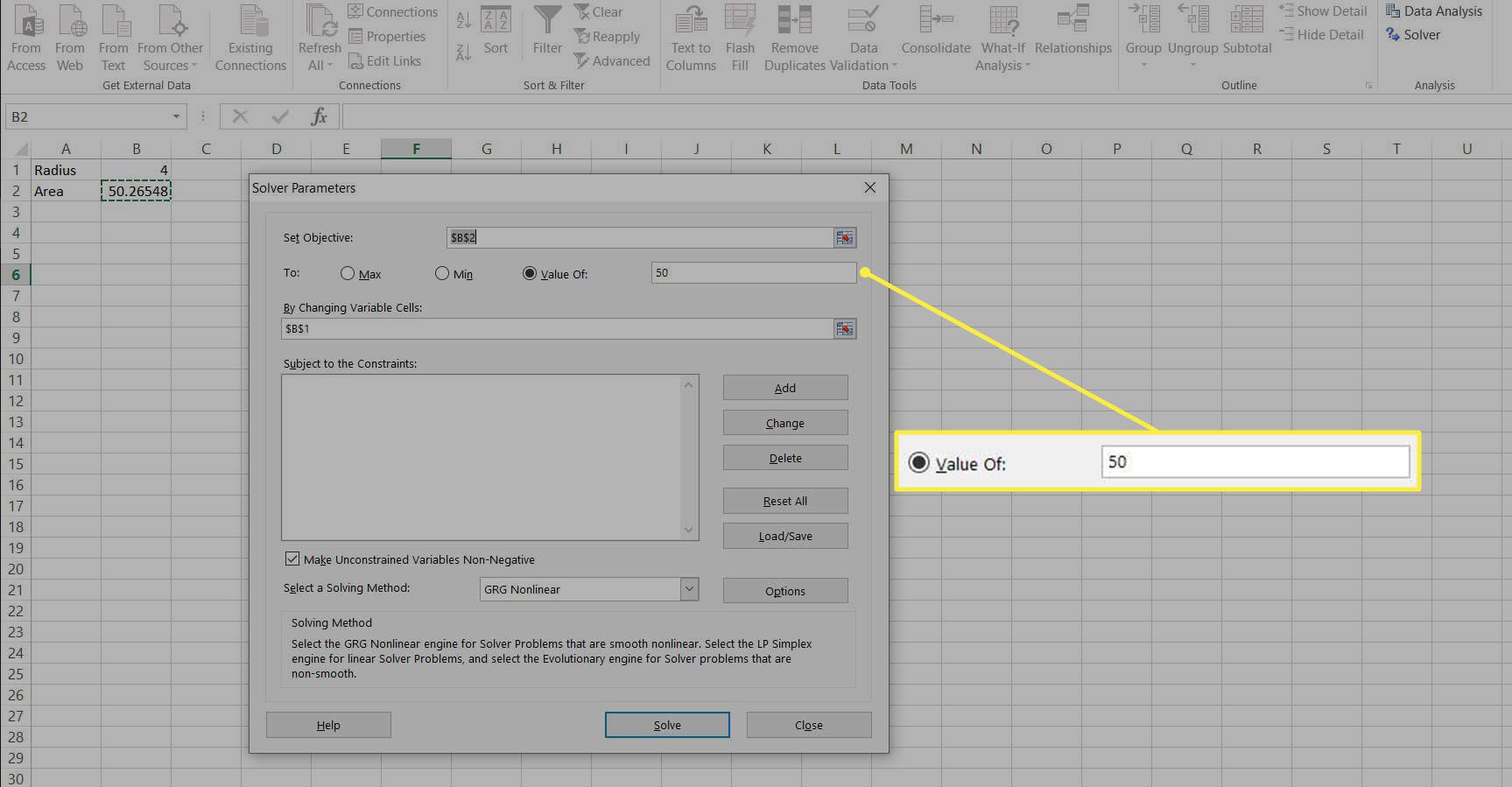
-
V poli s názvem Změnou proměnných buněk: zadejte buňku obsahující poloměr, B1.
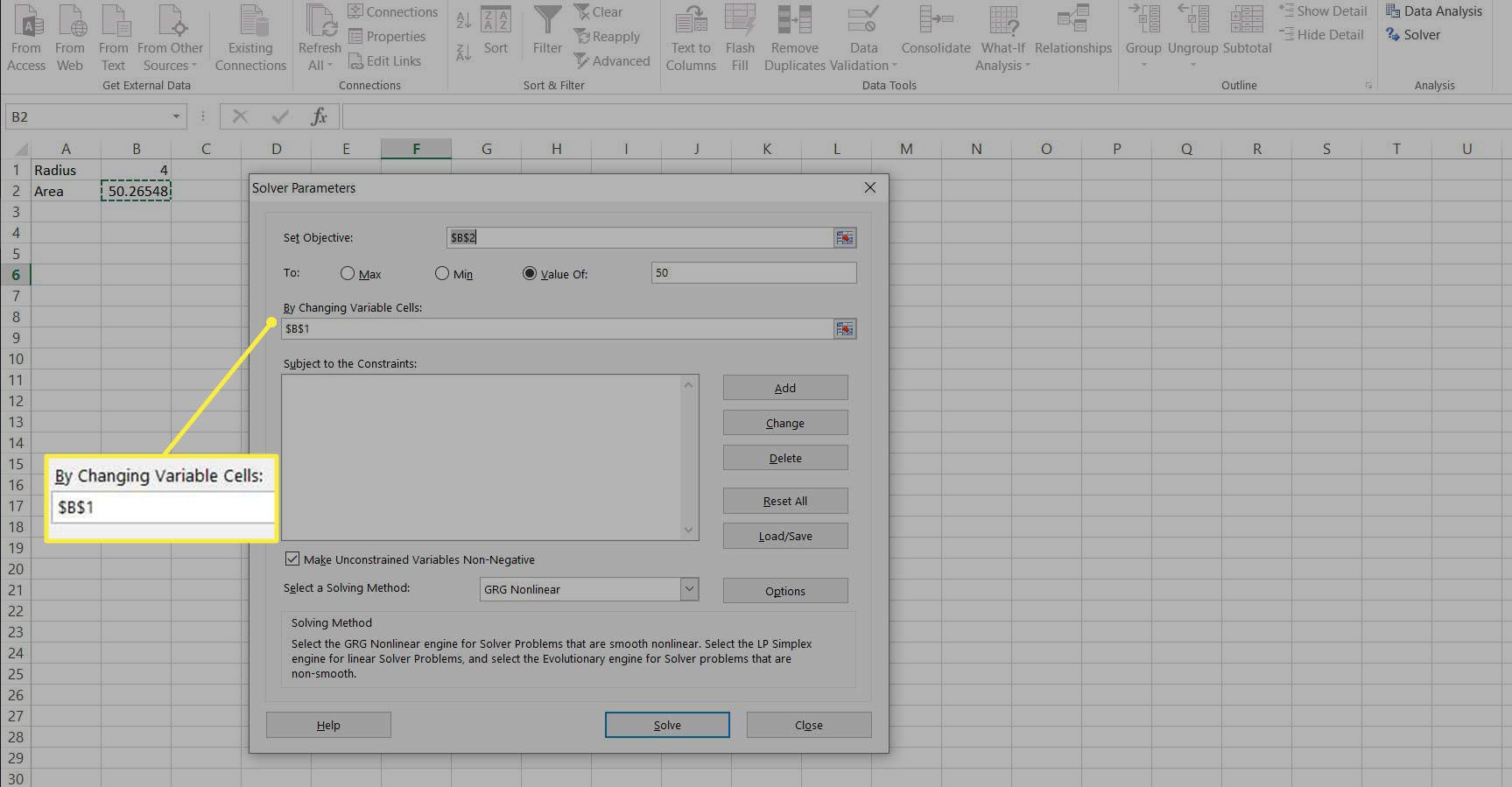
-
Ostatní možnosti ponechte ve výchozím nastavení a vyberte Řešit. Optimalizace se provádí, hodnota B1 se upravuje, dokud B2 není 50 a Výsledky řešitele Zobrazí se dialogové okno.
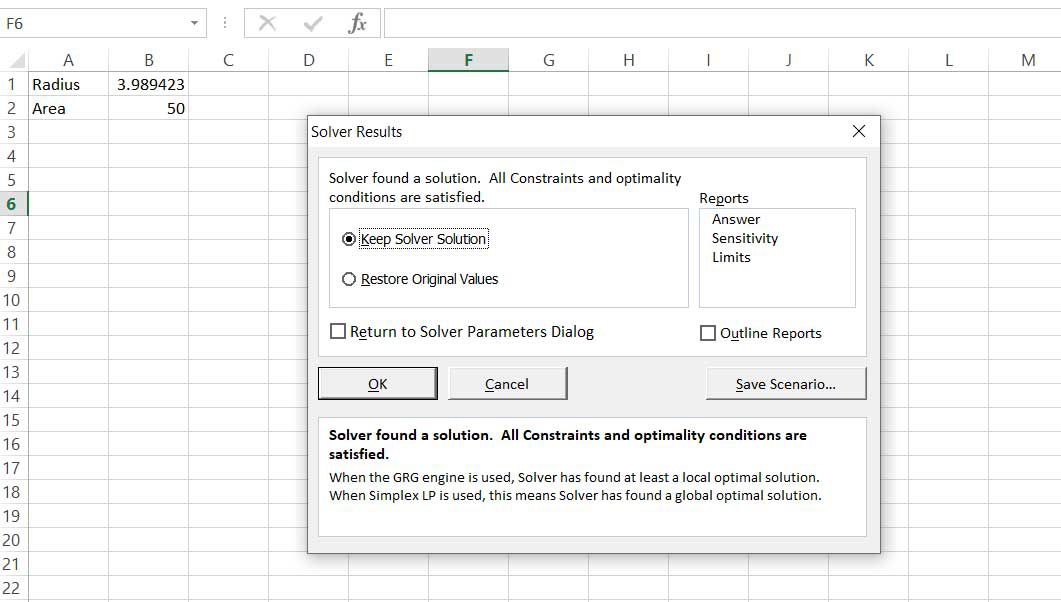
-
Vybrat OK ponechat řešení.
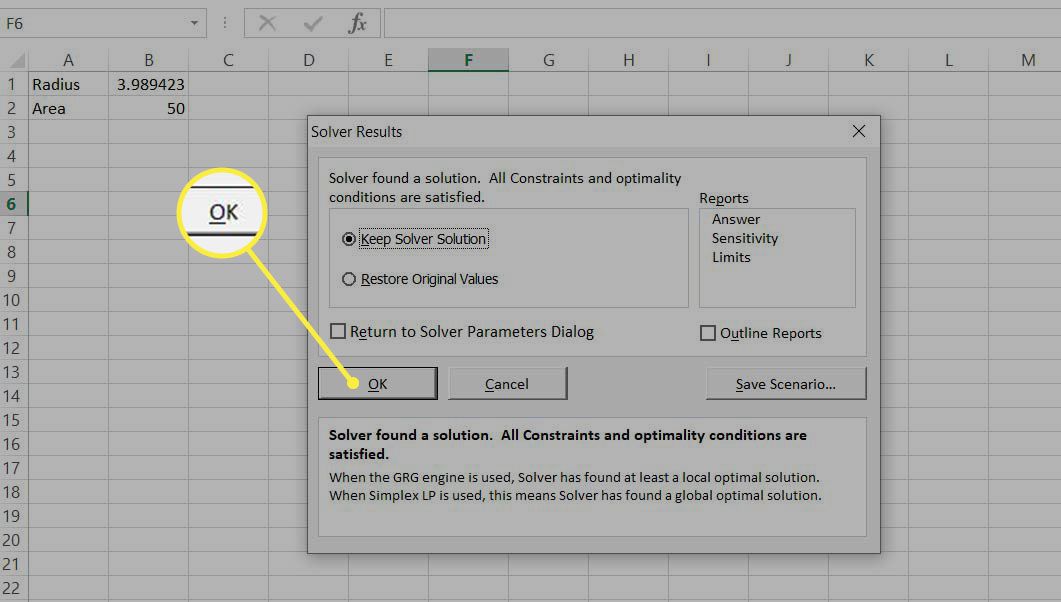
Tento jednoduchý příklad ukázal, jak řešič funguje. V takovém případě bychom řešení mohli snáze získat jinými způsoby. Dále se podíváme na několik příkladů, kde Řešitel poskytuje řešení, která by se jinak těžko hledala.
Přizpůsobení složitého modelu pomocí doplňku Řešič aplikace Excel
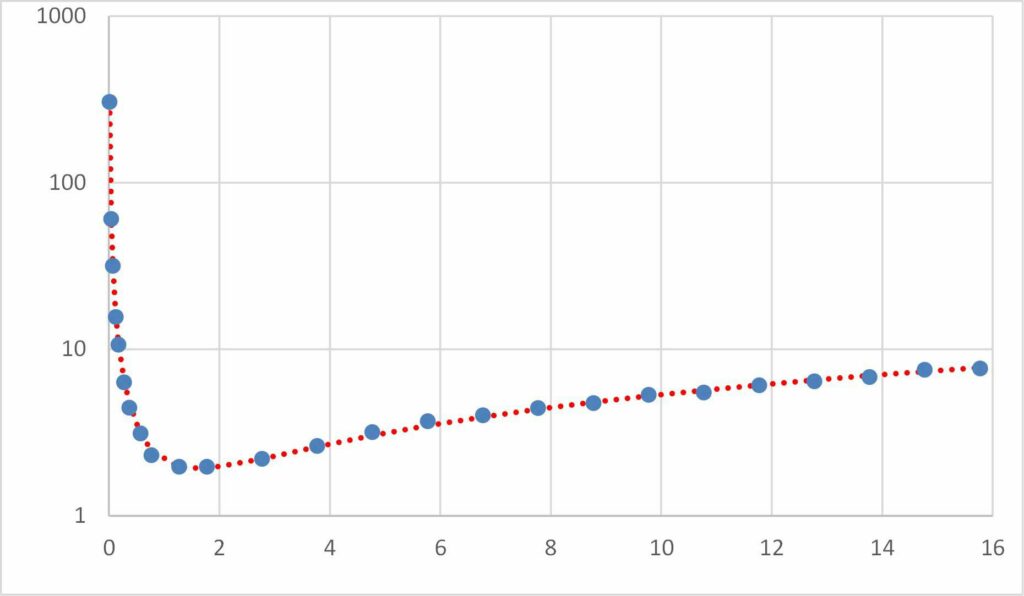
Excel má integrovanou funkci pro provádění lineární regrese, která prochází přímkou skrz sadu dat. Mnoho běžných nelineárních funkcí lze linearizovat, což znamená, že k přizpůsobení funkcí, jako jsou exponenciály, lze použít lineární regrese. U složitějších funkcí lze Řešič použít k provedení „minimalizace nejmenších čtverců“. V tomto příkladu budeme uvažovat o přizpůsobení rovnice tvaru ax ^ b + cx ^ d k údajům uvedeným níže.
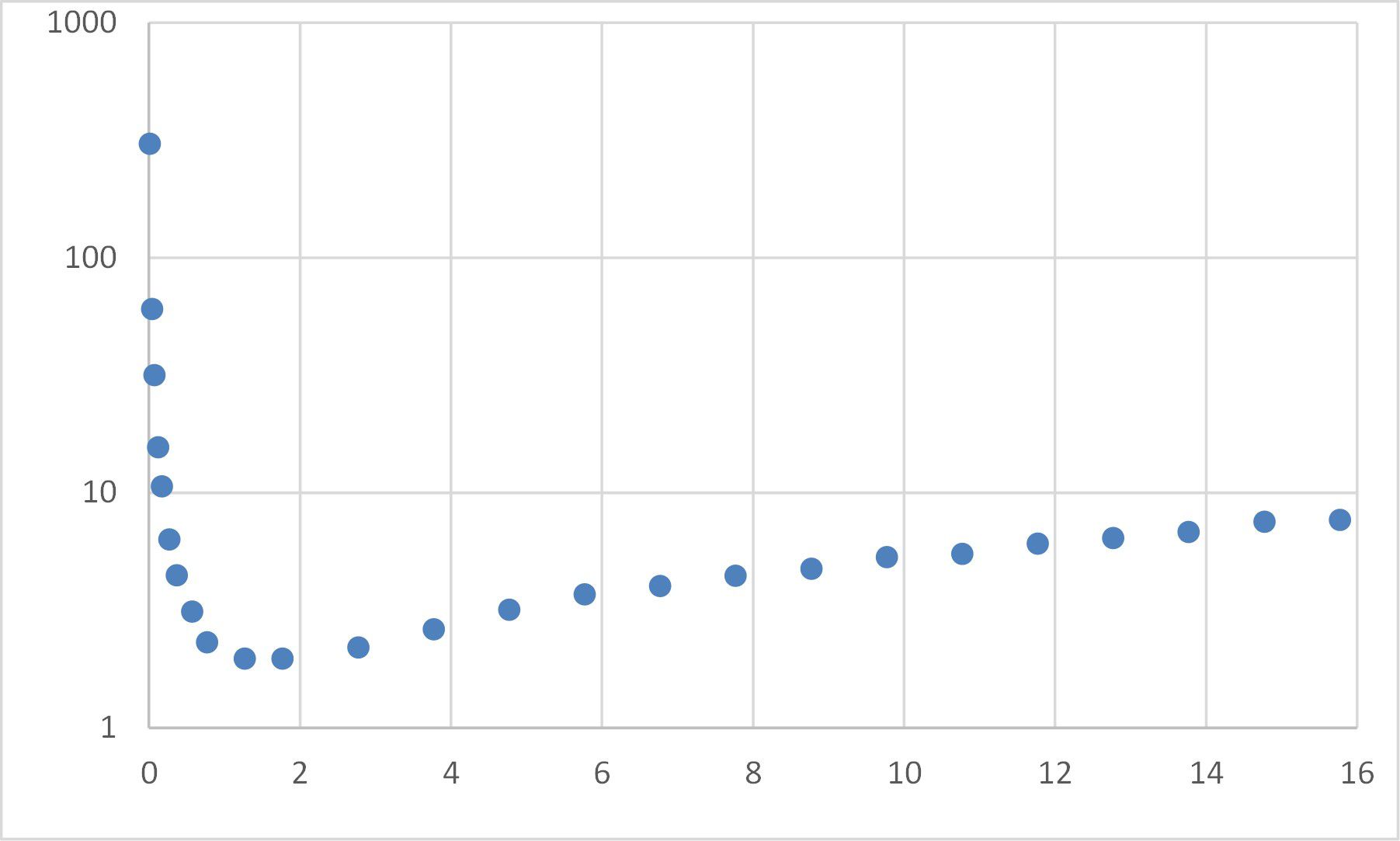
Jedná se o následující kroky:
-
Uspořádejte datovou sadu s hodnotami x ve sloupci A a hodnotami y ve sloupci B.
-
Vytvořte někde v tabulce 4 hodnoty koeficientů (a, b, c a d), kterým lze dát libovolné počáteční hodnoty.
-
Vytvořte sloupec přizpůsobených hodnot Y pomocí rovnice tvaru ax ^ b + cx ^ d, která odkazuje na koeficienty vytvořené v kroku 2 a hodnoty x ve sloupci A. Všimněte si, že aby bylo možné zkopírovat vzorec dolů do sloupce, odkazy k koeficientům musí být absolutní, zatímco odkazy na hodnoty x musí být relativní.
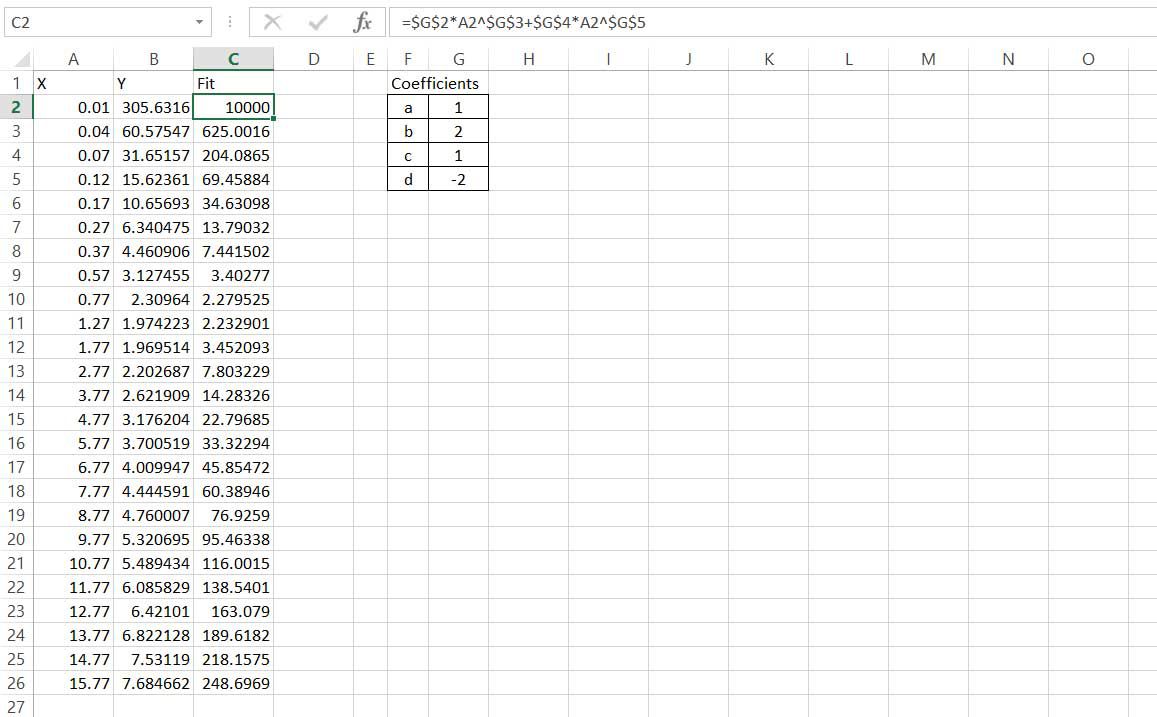
-
I když to není podstatné, můžete získat vizuální indikaci toho, jak dobrá je rovnice, vynesením obou sloupců y proti hodnotám x na jednom rozptylovém grafu XY. Má smysl použít značky pro původní datové body, protože se jedná o diskrétní hodnoty se šumem, a použít přímku pro přizpůsobenou rovnici.
-
Dále potřebujeme způsob kvantifikace rozdílu mezi daty a naší přizpůsobenou rovnicí. Standardní způsob, jak toho dosáhnout, je vypočítat součet čtvercových rozdílů. Ve třetím sloupci je pro každý řádek původní hodnota dat pro Y odečtena od přizpůsobené hodnoty rovnice a výsledek je na druhou. Takže dovnitř D2, hodnota je dána = (C2-B2) ^ 2. Poté se vypočítá součet všech těchto čtvercových hodnot. Protože jsou hodnoty na druhou, mohou být pouze kladné.
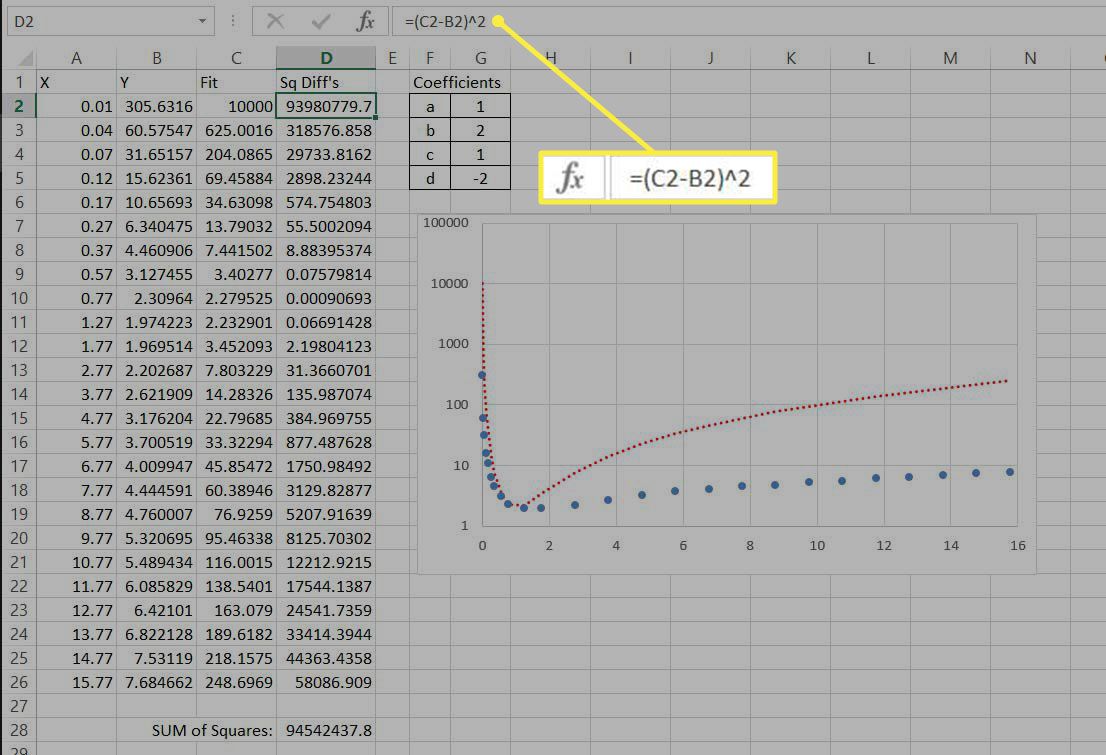
-
Nyní jste připraveni provést optimalizaci pomocí Řešitele. Existují čtyři koeficienty, které je třeba upravit (a, b, c a d). Máte také jednu objektivní hodnotu k minimalizaci, součet čtvercových rozdílů. Spusťte řešič, jak je uvedeno výše, a nastavte parametry řešiče tak, aby odkazovaly na tyto hodnoty, jak je uvedeno níže.
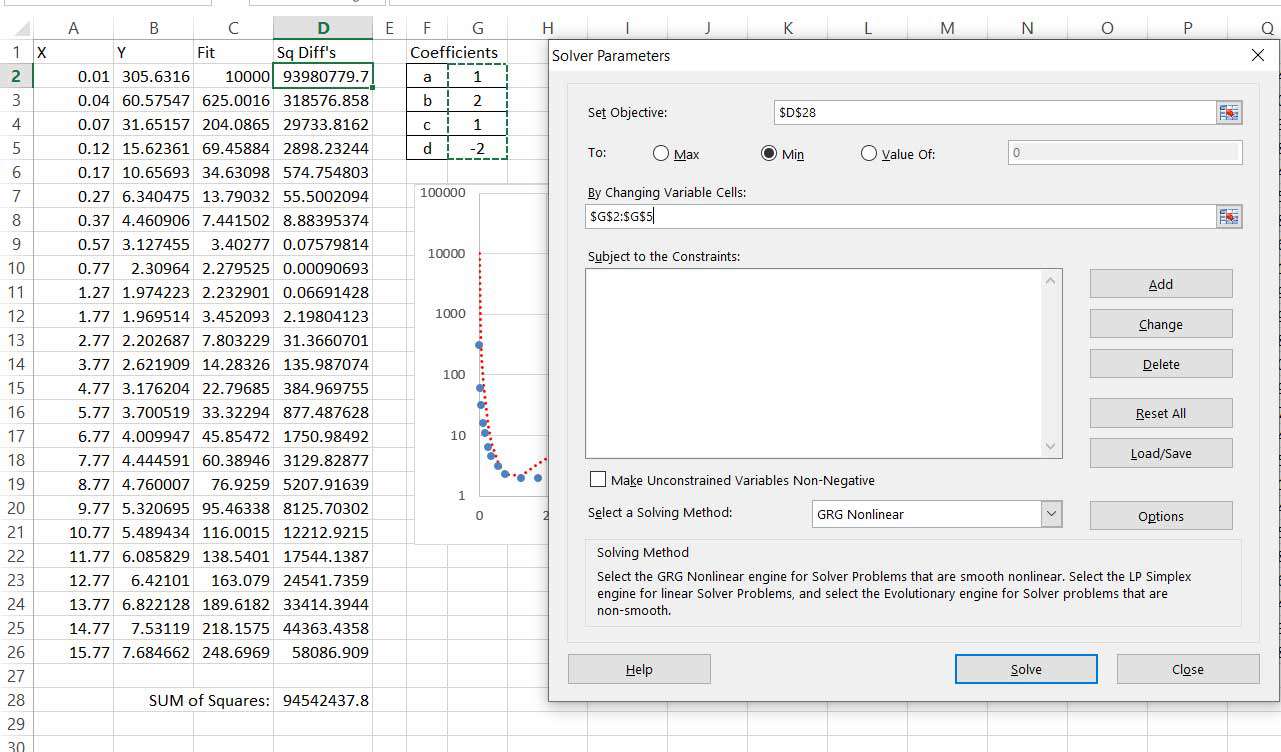
-
Zrušte zaškrtnutí možnosti Nastavit neomezené proměnné na nezápornéby to donutilo všechny koeficienty nabývat kladných hodnot.
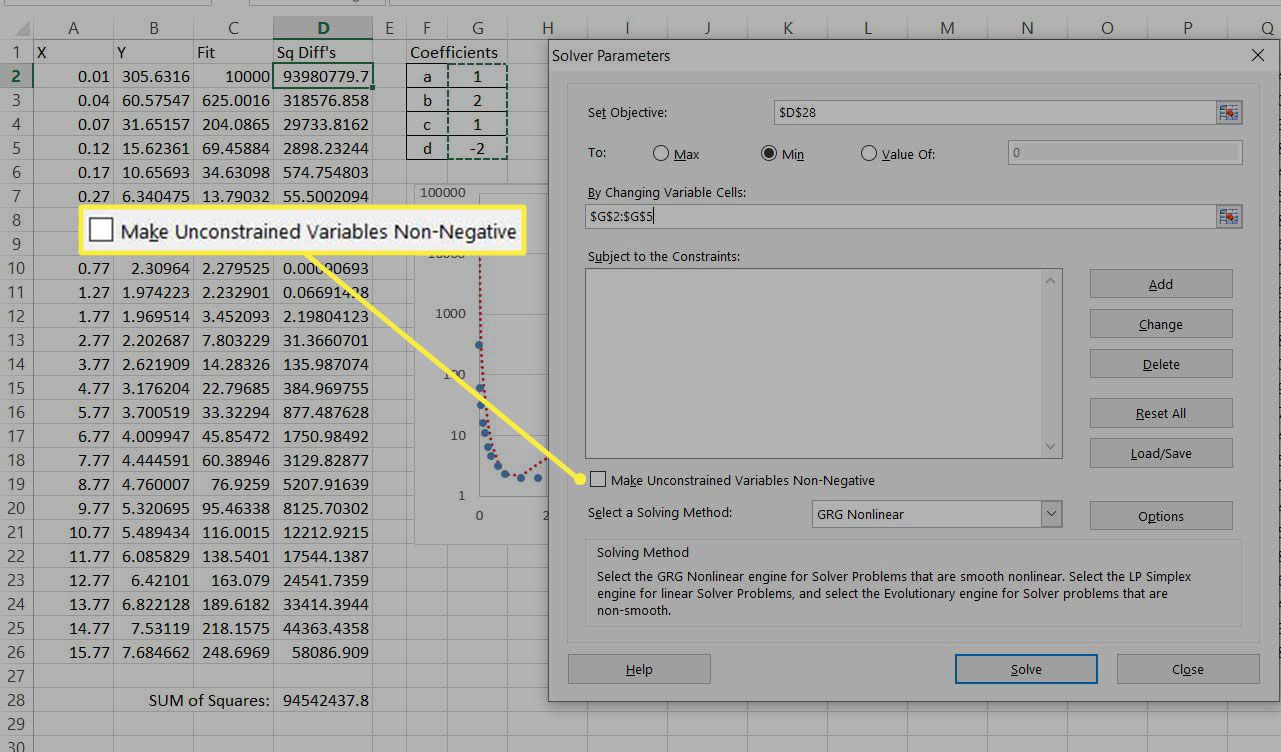
-
Vybrat Řešit a zkontrolujte výsledky. Tabulka se bude aktualizovat a bude dobře indikovat, zda je fit. Pokud řešič při prvním pokusu nevyhovuje, můžete jej zkusit spustit znovu. Pokud se přizpůsobení zlepšilo, zkuste to vyřešit z aktuálních hodnot. Jinak můžete před vyřešením zkusit ručně vylepšit přizpůsobení.
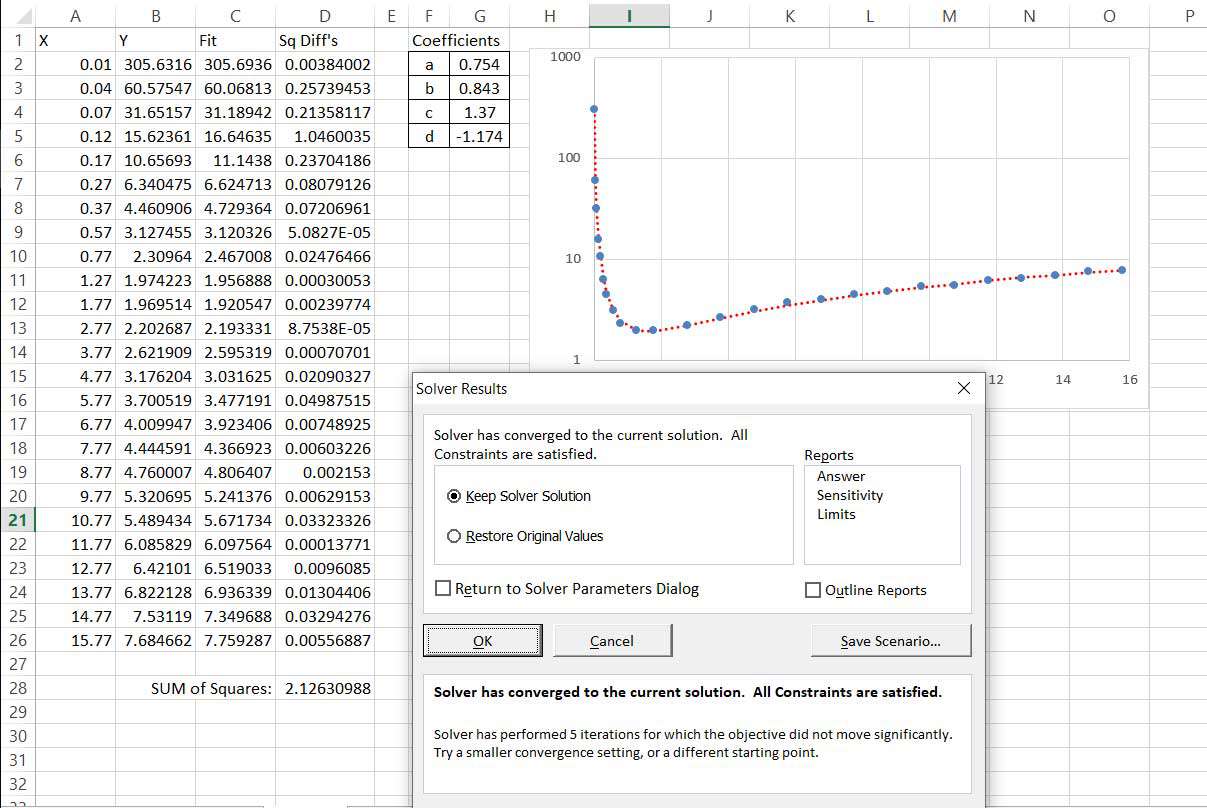
-
Jakmile získáte dobrou shodu, můžete řešitele opustit.
Iterativní řešení modelu
Někdy existuje relativně jednoduchá rovnice, která dává výstup z hlediska nějakého vstupu. Když se však pokusíme problém převrátit, není možné najít jednoduché řešení. Například energie spotřebovaná vozidlem je přibližně dána vztahem P = av + bv ^ 3 kde v je rychlost, a je koeficient valivého odporu ab je koeficient aerodynamického odporu. I když se jedná o poměrně jednoduchou rovnici, není snadné ji přeskupit, aby poskytla rovnici rychlosti, kterou vozidlo dosáhne pro daný příkon. Můžeme však použít Řešitel k iterativnímu nalezení této rychlosti. Například vyhledejte rychlost dosaženou při příkonu 740 W.
-
Vytvořte jednoduchou tabulku s rychlostí, koeficienty a a b a z nich vypočítanou sílu.
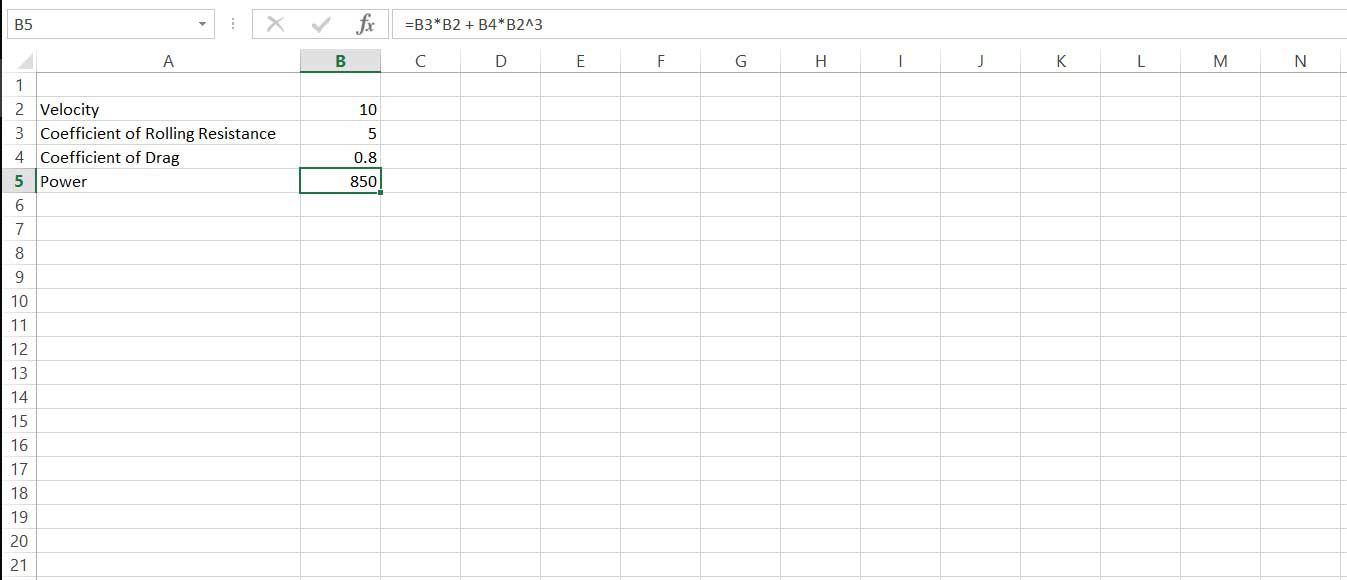
-
Spusťte Řešitel a zadejte sílu, B5jako cíl. Nastavte objektivní hodnotu 740 a vyberte rychlost, B2, jako proměnné buňky, které se mají změnit. Vybrat řešit spustit řešení.
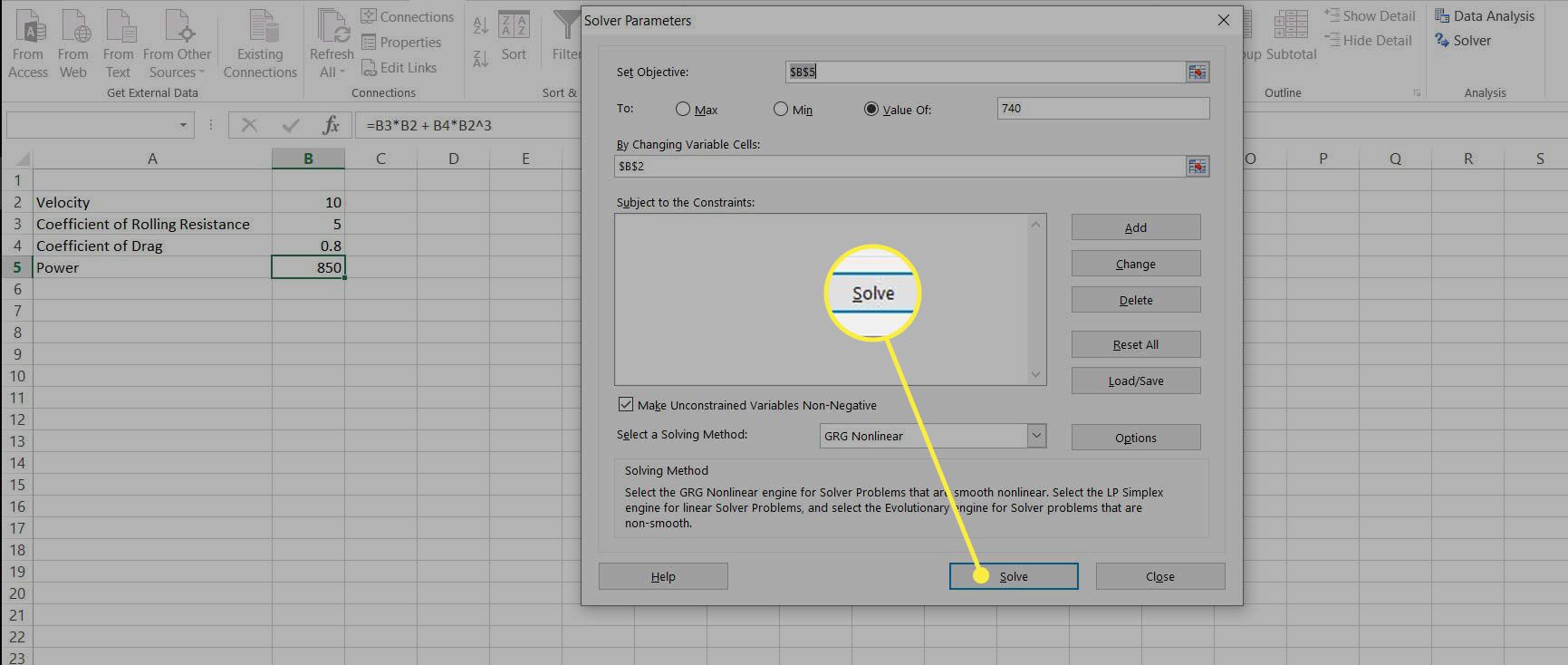
-
Řešitel upravuje hodnotu rychlosti, dokud není síla velmi blízká 740, a poskytuje požadovanou rychlost.
-
Řešení modelů tímto způsobem může být často rychlejší a méně náchylné k chybám než obrácení složitých modelů.
Pochopení různých možností dostupných v řešiči může být docela obtížné. Pokud máte potíže se získáním rozumného řešení, pak je často užitečné použít okrajové podmínky na vyměnitelné buňky. Jedná se o mezní hodnoty, nad které by neměly být upravovány. Například v předchozím příkladu by rychlost neměla být menší než nula a bylo by také možné nastavit horní mez. To by byla rychlost, o které jste si docela jisti, že vozidlo nemůže jet rychleji než. Pokud jste schopni nastavit hranice pro proměnlivé buňky proměnných, pak to také umožňuje lépe fungovat další pokročilejší možnosti, například multistart. Tím se spustí řada různých řešení, počínaje různými počátečními hodnotami proměnných. Výběr metody řešení může být také obtížný. Simplex LP je vhodný pouze pro lineární modely, pokud problém není lineární, selže se zprávou, že tato podmínka nebyla splněna. Další dvě metody jsou vhodné pro nelineární metody. GRG Nonlinear je nejrychlejší, ale jeho řešení může velmi záviset na počátečních počátečních podmínkách. Má flexibilitu, že nevyžaduje, aby proměnné byly nastaveny hranice. Evoluční řešič je často nejspolehlivější, ale vyžaduje, aby všechny proměnné měly horní i dolní hranici, což může být obtížné předem zpracovat. Doplněk Řešitel aplikace Excel je velmi mocný nástroj, který lze použít na mnoho praktických problémů. Chcete-li plně využít sílu aplikace Excel, zkuste kombinovat Řešitele s makry aplikace Excel.